Раздел: ВЗГЛЯД Тема: Автор: Александр ПОПОВ, эксперт
Механика в электронике
Окончание. Начало – в № 3-2023 Кронштейн – это в первую очередь балка с точки зрения сопромата. Главная формула расчета балки имеет, на самом деле, очень простой вид (можете блеснуть при случае в компании тем, что знаете, как считается балка на изгиб). Всего-то три составляющих в формуле. Считать балки не обязательно в каждом конкретном случае, но представлять, что чего означает, будет полезно. Итак, сама формула: Ϭ = М/W Ϭ – напряжение, измеряется в н/ м2, М – изгибающий момент, измеряется в нм, W – момент сопротивления, измеряется в м3. Вычисляем напряжение, испытываемое материалом, сравниваем с допустимым напряжением, которое является свойством используемого материала и определяется по справочникам. Еще существует такая вещь, как коэффициент запаса прочности, который задается, исходя из условий эксплуатации. Например, если эксплуатация связана с риском для жизни и здоровья человека (например, лифтовое оборудование), коэффициент запаса прочности чаще всего равен 5. Если это просто какой-нибудь подъемный кран, то 2,5. Каким он должен быть для кронштейна видеокамеры, с этим не сталкивался ни разу. Какой считаете нужным, такой и задавайте – не велика потеря, если что. Умножаем расчетное напряжение на коэффициент запаса прочности и сравниваем с допустимым. Если меньше допустимого, значит все хорошо. Если больше, то конструкцию надо усиливать. Вот и все, если в общем. А если в частности, то сложности начнутся с определения реального суммарного момента и момента сопротивления. Вот тут уже и логарифмы запросто могут появиться. Но мы ничего не будем считать, а только понимать. Изгибающий момент – это характеристика внешних воздействий – сил и плеч, на каких они действуют. А момент сопротивления – это характеристика уже самой конструкции, подверженной воздействию моментов внешних сил. В свою очередь, момент сопротивления W = I/r, где I – момент инерции сечения балки; r – расстояние до нейтральной оси. Нейтральная ось – это то множество точек, которые при изгибе не испытывают ни растяжения, ни сжатия. Становится понятно, что прочность балки является функцией ее геометрии. И помимо свойства самого материала, важнейшим параметром является момент инерции сечения. Для примера рассмотрим прямоугольное сечение (рис.6)
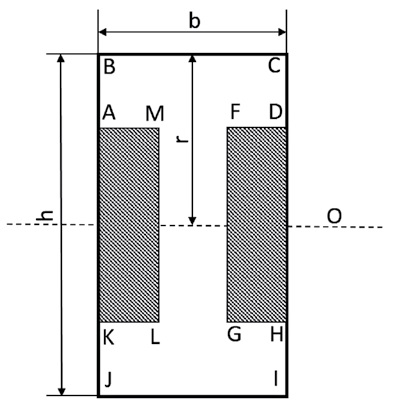
Рис.6 Ширина прямоугольника – b; высота – h. Очень рекомендую запомнить, чему равен момент инерции прямоугольного сечения: I = b x h33 / 12 Любой, кто когда-либо изучал сопромат, эту формулу помнит наизусть. Высотой в данном случае считается сторона прямо- угольника, находящаяся в плоскости приложения изгибающего момента. Если наш прямоугольник положим на бок, продолжая изгибать балку в вертикальной плоскости, то h и b в формулах поменяются местами. Для нас же важно понимание, что от высоты момент инерции зависит аж в кубической зависимости, а вот от ширины – только в линейной. А чем больше момент инерции сечения, тем меньше напряжение в балке (балка существенно мощнее в вертикальной плоскости при изгибе, нежели в горизонтальной). До недавнего времени я считал это просто очевидным для всех фактом, пока меня не попросили высказать свое мнение относительно именно кронштейна для камеры: как будет красивее – при вертикальном расположении прямоугольного сечения несущей балки или горизонтальном? Если решение безграмотное, говорить о его эстетике уже нет смысла. Попутно, если кому-то интересно: момент инерции круглого сечения: I = Πd4 /64 = Πr4 /4 И еще важное дополнение: момент инерции какого-то сложного сечения представляет собой сумму моментов инерции простых сечений, из которых составлено полное сечение. Причем, это правило справедливо и при вычитании одних сечений из других. Например, сечение кольца (трубы) может быть представлено как разность круглого сечения внешнего диаметра и круглого сечения диаметра внутреннего. При изгибе балки (рис.6) волокна, находящиеся над центральной плоскостью О будут испытывать растяжение, а те, что внизу этой плоскости, – сжатие (или наоборот, при изгибе в противоположную сторону). А волокна, находящиеся в самой этой плоскости, не будут испытывать никаких нагрузок. Пересечение этой горизонтальной плоскости с сечение носит название нейтральной оси. Формула расчета балки на изгиб принимает вид: Ϭ = М х r/I М – изгибающий момент, приложенный к балке; I – момент инерции сечения; r – расстояние до нейтральной оси. Из формулы понятно, что при r=0 – на нейтральной оси напряжение равно нулю. Далее, по мере удаления от нейтральной оси напряжение будет возрастать и достигнет своего максимума на краю сечения. Ввиду неравномерности напряжения нет смысла делать ее равнопрочной по всему сечению балки, если внешние силы имеют заведомо известное направление. Есть возможность сильно облегчить конструкцию без ущерба для ее прочности. И, конечно, ощутимо снизить расход материала. В качестве примера на рис. 6 без существенного снижения прочности можно «вырезать» четырехугольники АМLК и DFGH. В результате получим одну из самых популярных балок – двутавр (две буквы «Т» навстречу друг другу). Именно поэтому железнодорожные рельсы имеют не сплошное сечение, а двутавровое. По этим же соображениям (убрать ненагруженные элементы из сечения) существуют и тавровые балки, и швеллеры и даже простейший уголок, используемый в качестве балки. На рис. 3 (см. начало – № 3-2023) кронштейн имеет именно двутавровое сечение. Судя по внешнему виду, очень мощный кронштейн. И отверстия в площадке выполнены грамотно. Ему бы площадку чуточку побольше, цены бы не было. Но нам мало иметь просто механическую прочность, чтобы кронштейн не сломался, а камера не свалилась бы со штатного места. Нам недостаточно даже сохранить направление обзора. Необходимо исключить любую вибрацию с амплитудой, выше допустимой, чтобы камера могла реализовать свои возможности по разрешающей способности в полном объеме. В большинстве случаев основу кронштейна составляет балка. И нередко только она (рис.7).
Рис.7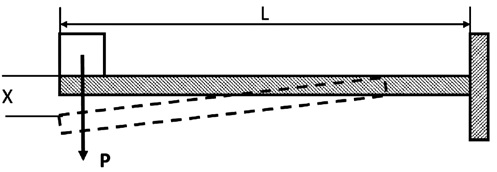
Рис.8 Балка, закрепленная только с одного конца, называется консоль (рис.8). С одной стороны, если говорить о кронштейне, это самый простой вариант. С другой, как говорят, «простота хуже воровства». Именно как кронштейн консоль – вещь весьма коварная. И «коварство» это обусловлено т.н. правилом Верещагина. Если совсем упрощенно, то Х ~ P L3 /I Где Х – смещение на конце консоли, L – длина консоли, P – сила, приложенная на конце консоли , I – момент инерции сечения консоли.
То есть, смещение на конце консоли пропорционально кубу длины. А об этом очень часто забывают. Стандартная ситуация – длины кронштейна не хватает, чтобы в сектор обзора камеры не попала водосточная труба или какие-то архитектурные элементы на стене здания. И стандартное же решение – крепление штатного кронштейна к концу консоли, сделанной «на скорую руку» из трубы прямоугольного сечения. Потом удивление по поводу невозможности настройки резкости, «обвинение» объектива, попытка его замены и снова удивление. В действительности надо было изготавливать совершенно новый кронштейн для заданного выноса с совершенно другими конструктивными элементами. В любом случае, при наличии нагрузки какое-то смещение на конце будет иметь место. Просто для штатного кронштейна оно настолько мизерное, что обеспечивает реализацию характеристики камеры по разрешающей способности. Но как только мы консольно увеличиваем длину, скажем, в два раза, это смещение увеличивается в 8 раз; для троекратного увеличения длины смещение возрастет уже в 27 раз. И чтобы компенсировать такую резко возросшую возможную амплитуду вибрации на конце, необходимо в первом случае увеличить момент инерции сечения в 8 раз, а во втором – в 27. Увеличение момента инерции сечения – в первую очередь увеличение геометрических размеров. А это повлечет за собой резкое увеличение веса, а, значит, увеличение, в том числе, и опорной площадки по всем измерениям. Поэтому задача снижения амплитуды колебаний на конце решается в подобных случаях установкой так называемых подкосов в плоскостях всех возможных внешних сил (рис.9).
Рис.9 На фото представлен реально существующий на объекте вариант установки камеры на консоли. Вряд ли установленные подкосы явились результатом каких-то расчетов, судя по тому, что выполнены они из того же профиля, а, значит, имеют ту же механическую прочность, что и сама консоль. Да и место стыковки подкосов с консолью вызывает вопросы, поскольку все еще остается достаточно большой вылет самой консоли в свободном виде. Но очевидно, что даже такая малогабаритная камера с малым весом потребовала очень серьезных дополнительных мер для обеспечения жесткости установки при большом вылете консоли. Чем дальше от площадки консоли отнесены площадки подкосов, тем меньше подкосы будут испытывать напряжения на изгиб, а все больше – на растяжения и сжатия. А эти допустимые напряжения просто несопоставимы с изгибающими. Поэтому при грамотной установке подкосов нет необходимости делать их такими же в сечении и материале, как и консоль. Новая конструкция тоже потребует расчетов, если не хотим столкнуться с очередными сюрпризами сопромата. Если по какой-либо причине теоретическое решение невозможно, следует практическими испытаниями проверить макетный образец, прежде, чем устанавливать камеру на штатное место. В противном случае нередко имеем дело с нагромождениями всевозможных конструкций в месте установки камеры, отличающихся кошмарным внешним видом и безграмотностью инженерной мысли. Что и подтверждает фото (рис.9). Понимание «коварства» консоли важно еще и с точки зрения оценки самого места установки камеры. Даже если камера со штатным кронштейном представляют собой совершенно правильную и сбалансированную систему, само место установки способно эту «правильность» разрушить. Просто вертикальный столб может представлять собой классическую консоль для боковых сил (ветровые нагрузки, динамические колебания). С одной стороны, чем выше будет установлена камера, тем существенно эффективней может оказаться наблюдение с точки зрения минимизации теневых зон. Но и от смещения пропорционально кубу высоты никуда не деться. И подкосы на столбы не поставишь. Поэтому всегда надо задуматься об объективных ограничениях в каждой конкретной ситуации – не все может пойти во благо, даже, если это и технически возможно. И такое было в нашей практике – на мощнейших опорах освещения были установлены видеокамеры на двадцатиметровой высоте. Для прожекторов амплитуда колебаний и в полметра, и даже в метр абсолютно не принципиальна. Зато нам на существенно меньшей высоте наших камер, нежели установлены прожекторы на этих опорах, резкости видеоизображения добиться так и не удалось. Существуют решения установки видеокамер даже на кораблях с возможностью эксплуатации и на ходу, и на волнении. Мне приходилось их видеть. Но уверяю, это совсем не типовое решение для нашего рынка – камера устанавливается на гиростабилизированном основании. Главные свойства гироскопа – сохранение положения в пространстве (в пределах незначительного дрейфа) и устойчивость к ударным нагрузкам. Но стоимость такого решения сделает его просто абсурдным для всех типовых задач рынка. Цена простейшего гиростабилизатора для видеосъемки с рук начинается от 200 000 рублей. И для полноты картины следует еще остановиться на всевозможных оттяжках при установке кронштейнов. Это первое, что приходит в голову, когда обеспечить должную жесткость установки камеры не удалось. Именно в отношении консоли такие решения встречаются чаще всего. И горизонтально расположенных, и вертикально. И, как правило, без какого-либо положительного результата. Потому что тросовая оттяжка, как и консоль, – вещь не менее специфическая. Во-первых, работа с оттяжками требует совершенно конкретных технологий – любое крепление к конструкции осуществляется только через т.н. коуши или с помощью такелажных скоб. Никакие узлы на тросах не допускаются. Только специальными зажимами под конкретный диаметр троса. Во-вторых, каждое такое крепление потребует расчета расположения мест крепления и на поверхности установки кронштейна, и на самом кронштейне, допустимых нагрузок на трос или выбор троса в зависимости от нагрузки и т.п. А самое главное, что невозможно измерить реальную нагрузку на трос, которая в разы отличается от разрывной для обеспечения длительной и устойчивой эксплуатации. Допустимая нагрузка определяется по формуле P= R/K Где R – разрывное усилие, а К – коэффициент запаса, определяемый условиями эксплуатации. Например, разрывное усилие стального троса диаметром 2 мм составляет 2,35 кН (килоньютонов), а допустимая нагрузка – 0,47 кН; для троса диаметром 4 мм рабочая допустимая нагрузка составляет 1,88 кН при разрывной – 9,41. И эксплуатироваться растяжка должна именно при допустимой нагрузке, которую в нашем случае измерить вряд ли получится. Условия эксплуатации могут накладывать серьезные ограничения и по типу троса, и по срокам эксплуатации. Если это эксплуатация под открытым небом, то обычный стальной трехмиллиметровый трос «проживет» от силы года три. Нужен нержавеющий или в ПХВ-оболочке. Любой трос имеет первоначальное вытяжение. Кто хоть раз ставил новые струны на гитару, хорошо знает, что в течение первого дня придется настраивать инструмент через каждые пару часов. Кроме того, каждый металлический трос подвержен существенным температурным расширениям и сжатиям. Настанет зима – для обеспечения рабочей нагрузки придется натяжение ослабить, чтобы не началось разрушение, а летом, наоборот, надо будет снова трос натянуть. Ездить по объектам и крутить талрепа, причем, исключительно «на глазок»? Кто-нибудь готов этим заниматься? И самое главное! Колебания растяжками не ликвидировать. Потому что любой натянутый трос – это струна, которая создана как раз для того, чтобы колебаться. Сделаете частоту колебаний 440 Гц, получите ноту «ля». Почему растяжка – это струна? Для очень многих моих собеседников с нашего рынка явилось откровением то, что усилие натяжения прямой линии равно бесконечности. Для меня этот факт был всегда практически очевидным, поэтому решил на нем остановиться (рис.10)
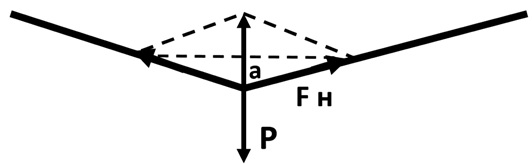
Рис.10 Любой трос имеет собственный вес Р, приложенный в некоторой точке весового среднего. Если трос однородный, то к центру отрезка этот вес Р уравновешивается суммой сил натяжения Fн, приложенных в этой же точке. Сумма находится по правилу параллелограмма, а поскольку силы натяжения одинаковы в одну и другую стороны, то параллелограмм превращается в ромб, и: Р= 2 Fн Cos a. Тогда Fн = Р/2 Cos a При положении троса без провиса угол «а» равен 900, соответственно Cos a= 0, тогда Fн = ∞ Вот и все. Поэтому провис, пусть и не заметный глазу, будет присутствовать всегда. А может быть и заметный при очень большой разрывной нагрузке троса и большом усилии натяжения. И всегда будут присутствовать колебания. Любой более-менее грамотный моряк знает, что при морской буксировке (когда одно океанское судно тащит другое на буксире), если буксирный трос вышел из воды, надо мгновенно падать за какое-нибудь мощное препятствие, потому что неминуемо последует обрыв буксирной линии с сокрушительными разрушениями, ею создаваемыми. Там провис измеряется метрами при разрывной нагрузке на трос.
Не стоит забывать о бесконечном усилии натяжения горизонтали и при организации воздушных кабельных линий – выбирать трос, исходя из действительного веса кабеля, а не «на глазок», и не пытаться вытянуть линию в максимально горизонтальную – сначала разорвется несущий трос, а следом мгновенно оборвется сама линия. И с растяжками мы имели собственный опыт. Для установки поворотных камер с мощными трансфокаторами все на том же стадионе «Петровский» были изготовлены специальные сварные конструкции в виде усеченных пирамид, которые крепились к горизонтальной поверхности трибуны. А жесткость конструкции попытались обеспечить именно тросовыми растяжками. Наша затея успеха не имела – от вибрации камер нам уйти не удалось. Но мы всегда анализировали собственный отрицательный опыт, находили причины и не допускали впредь подобное. С той же целью и написана эта статья – проанализировать типичные ошибки и дать возможность монтажникам и проектировщикам не наступать на заведомые «грабли», а производителю не создавать заведомо безграмотные товары. Кроме всего прочего, на камеру на кронштейне может воздействовать еще и вращательный момент внешних сил, в результате чего камера может испытывать вращательные колебания вокруг оси кронштейна. На этом мы подробно останавливаться не будем, поскольку случай этот довольно редкий и связан с совсем уж хлипкой конструкцией кронштейна. Хотя формулу для расчета такого возможного угла поворота привести можно: φ = (М L)/(G Ip) φ — читаем «Фи» – угол закручивания в радианах, М — закручивающий момент, L — длина кронштейна, G — читаем «Ж» – модуль Юнга, Ip — читаем «Ип» – полярный момент инерции. А теперь, если вы дочитали до этого места, сможете легко запомнить эту формулу на всю жизнь. Пусть не будете никогда считать по ней свои кронштейны, зато незаурядными знаниями сопромата сможете блеснуть в любой компании. Потому что по первым буквам: «Если хочешь быть «фифой», то сверху «мой» «лицо», а снизу «Ж» «Ип»». Вот так нам давал сопромат профессор Гаврилов. Как ни крути, он был прав, утверждая, что настоящего инженера без сопромата не бывает. А точнее, никуда от сопромата инженеру не уйти. Даже если он – инженер-электронщик.
Внимание! Копирование материалов, размещенных на данном сайте допускается только со ссылкой на ресурс http://www.tzmagazine.ru Рады сообщить нашим читателям, что теперь нашем сайте работает модуль обратной связи. Нам важна ваша оценка наших публикаций! Также вы можете задавать свои вопросы.Наши авторы обязательно ответят на них. Ждем ваших оценок, вопросов и комментариев!

Добавить комментарий или задать вопрос

Правила комментирования статей

Версия для печати

Средняя оценка этой статьи: 0  (голосов: 0)
Ваша оценка: